.375 as a Fraction: Easy Decimal to Fraction Conversion

Let’s talk about a small math puzzle that often trips folks up—turning the decimal .375 into a fraction. Sounds basic, right? But there’s more going on than just the steps—there’s a story here about how we learn, how we remember, and yes, how we sometimes get fussy with tiny numbers.

Why .375 Matters

Decimals like .375 pop up in all sorts of real-world settings—cooking measurements, construction layouts, even when reading your phone’s screen size. Having a solid understanding of how to convert decimals to fractions—and why—is a kind of everyday math literacy. It’s not just a rote trick; it’s a way to stay fluent across different ways we represent numbers.

The Long-ish Road to 3/8

Here’s the usual conversion route:

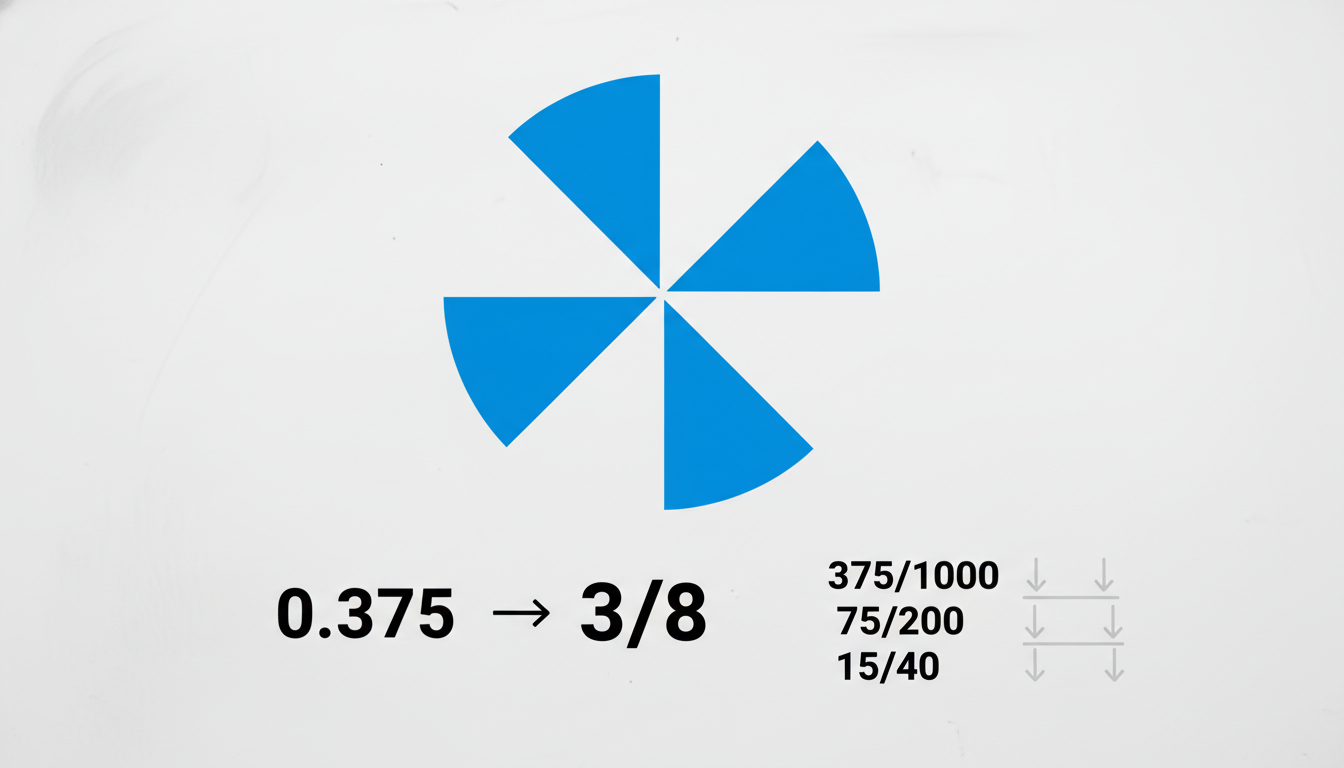
1. Start with .375, typically written as 0.375/1.
2. Because there are three digits after the decimal, multiply numerator and denominator by 1,000 → that gives 375/1000.
3. Simplify by dividing both by their greatest common divisor (GCD), which here is 125. That gives 3/8.

This method is clear, consistent, and favored by educational resources like MooMooMath , Cuemath , and Calculateme.com .

But Wait—Can We Do It Differently?

Yeah, you kinda can break it down faster if you’re fluent with fractions:

• You know that .125 = 1/8.
• And .375 is just three times that. So, multiply 1/8 by 3 to get 3/8.

Or, from a construction site chat I stumbled across:

“Multiply the decimal by the denominator you’re using—.375 × 16 = 6/16, which reduces nicely to 3/8.”

So there’s more than one path, depending on where you come from—whether it’s classroom method, mental math shortcuts, or real-world trade conversations.

Deep Dive: Why Fraction Simplification Matters

Simplifying Isn’t Just for Class—It Cuts Mistakes, Too

Simplified fractions are cleaner, easier to compare, and just generally less prone to slip-ups. Fraction tools like those at FormulaForge stress that reducing to lowest terms is a core habit—whether you’re doing algebra or everyday math .

Recognizing Patterns Is the Real Win

When you’re familiar with common decimal-fraction pairs—like .125, .25, .375, .5, etc.—you can do conversions mentally. You also notice familiarity when you see the same numbers in different places—say construction notations or cooking instructions.

Learning Multiple Methods Builds Flexibility

Being able to choose a method—systematic GCD calculations, scaling by powers of ten, mental shortcuts, or hands-on trade strategies—empowers real-world problem-solving. It’s one thing to know the rule; it’s another to pick the best tool for the moment.

Quick Summary

• Decimal .375 can be converted to a fraction most often—and correctly—as 3/8.
• Standard conversion is: .375 → 375/1000 → simplify via GCD 125 → 3/8 .
• Shortcut: Recognize .375 as three times .125 (which is 1/8).
• Field trick: Multiply by 16 (common in construction) to get 6/16 → 3/8 .

FAQs

Q1: Is .375 always equal to 3/8?
Yes. Whether you go through 375/1000 reduced by 125 or spot the pattern with eighths, you’ll land on 3/8.

Q2: Why multiply by 1,000 when converting?
You shift the decimal three places to turn .375 into a whole number in the numerator while keeping equivalence intact.

Q3: How do you find the GCD fast?
You can prime-factor both numbers (e.g., 375 and 1,000 both include 5³), or use the Euclidean algorithm to find the greatest common divisor quicker .

Q4: What’s the benefit of simplified fractions?
They’re easier to work with, less error-prone, and preferred in formal math—so you avoid that messy 375/1000 mess.

Q5: Are there other handy decimal-to-fraction conversions?
Absolutely—.25 is 1/4, .75 is 3/4, .125 is 1/8, etc. Recognizing these helps speed up mental calculations.

Final Thoughts

Converting .375 to a fraction may feel trivial, but it’s a small example of how we build numerical fluency. Whether through classroom routines, mental shortcuts, or on-the-job tricks, knowing that .375 is 3/8 can open doors to faster understanding, fewer errors, and smarter math moves.